デュレーションの解説-1- 住宅ローン支払額を簡単に求める方法

当社の扱う業務では「デュレーション」を扱う機会が多くあります。
企業担当者に「デュレーション」とは何かをわかりやすく説明するのは結構難しく、なんとか分かりやすい説明はないものかと考える機会が多いのですが、今回のコラムでは、できるだけ分かりやすく「デュレーション」を説明し、どのような業務で実際に活用できるのかを解説していきたいと思います。
住宅ローン支払額を簡単に求める方法
第1回の今回は、まずはデュレーションを理解してもらうために、身近な例として、住宅ローンの毎月の返済額をデュレーションの考え方を用いて簡単に求める方法を紹介します。
一例としまして、住宅ローンの借り入れ金額が1,200万円、毎月固定の返済期間20年、固定金利で借りる場合を考えます。仮に金利が0%だと仮定すると、毎月の返済額は1,200万円÷(20年×12ヶ月)=5万円となることは簡単に計算できます。
それでは、金利が1%の時の毎月の返済額は幾らになるでしょうか。厳密に計算するのは専門的な知識が必要で、終価率表というものを使ったり、エクセルで複雑な計算をさせたりする必要があります。
実は概算で数値を求めるのは、デュレーションの考え方を知っていれば簡単にできます。結論から先に示すと、5万円×(1+10年×1%)=5万円の10%割り増し=5.5万円となります。
金利が0%から2%への増加する場合返済額は約20%割り増し、金利が0%から3%への増加なら約30%割り増しとなります。
なぜこのような結果になるのかは、デュレーションに下記の異なる2つの性質があることを知ることで理解ができます。
| デュレーションの2つの性質 |
|---|
| (1) 平均の支払期間を表す (平均すると何年後に支払いがあるか) |
| (2) 金利感応度を表す (1%の金利変動に対して何%支払い額が変動するか) |
(1)から、20年間毎月同額の返済の場合「現在から平均何年後に返済するか」は現在から20年後までのちょうど中間である10年となり、デュレーションは10年となります。(下記図1参照)
図1:住宅ローン返済額のデュレーション
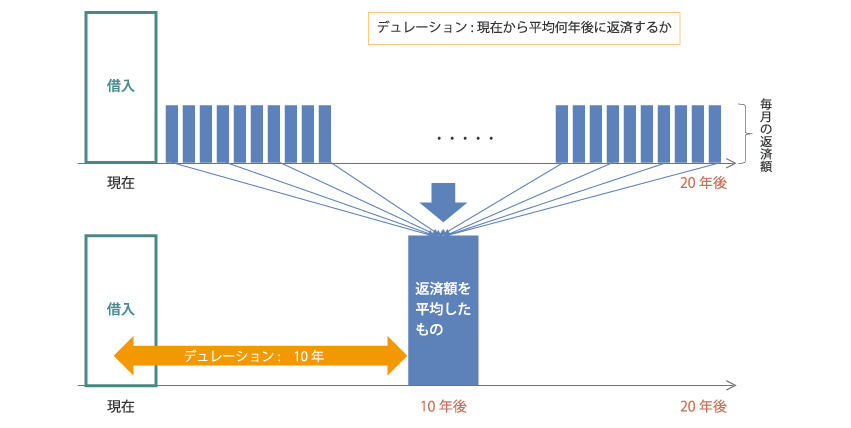
さらに、(2)から、デュレーション=金利感応度が10となるので、1%の金利上昇に対して返済額は10%増加するということになります。
返済期間を変えても同様の考え方ができ、返済額が一定(元利均等返済)の場合の住宅ローン返済額(毎月の返済額、及び返済総額)は、金利が1%上昇すると、およそ(返済期間÷2)%増加することになります。
実は、デュレーションにもいくつか種類がありまして、より正確には(1)はマコーレー・デュレーション、(2)は修正デュレーションということになりますが、両者の数値は近似しているため、概算値を考えるためには、両者を区別しなくても十分としました。
次回は、年金制度設計や年金資産運用の業務で登場する「デュレーション」について解説します。
※当コラムには、執筆した弊社コンサルタントの個人的見解も含まれております。あらかじめご了承ください。
あわせて読みたい記事はこちら







