割引率の話題から-1- スポットレート（イールドカーブ）の話

● 金利を見に行くときに、「スポットレート」の「イールドカーブ」を参照
● 「複数割引率」もしくは「単一の加重平均割引率」を選択適用
● これまで一般的に使用されていた「平均残存勤務期間」は使わず、「給付までの期間を給付金額により加重平均した期間（デュレーション）」を使用

また、これらの変更の際には、期末時点の利回りの割引率への反映方法や、重要性基準の対応など、実務も再考する必要が生じました。

今回はこの中でスポットレートのイールドカーブについて解説したいと思います。

旧基準では、たとえば平均残存勤務年数が10年であれば、残存10年の国債・社債の利回りを見に行くことが多かったかと思います。

ところで、わが国で流通しているほとんどの債券は利付債となっており、毎年の利払い（クーポン）がついています。これらの債券の利回りの求め方を見てみましょう。

まず、利回りrとしたときに、t年後の価格と現在の価格の関係は、複利計算で次のようになります。

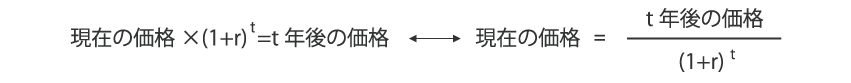
そこで債券の売買価格が、クーポンや元本の現価と一致していると考え、債券価格P、毎年のクーポン（利息）C、額面Fとすると、償還まで10年の債券であれば次のような算式が成り立ちます。（以下簡略のため、残存10年で説明します。）

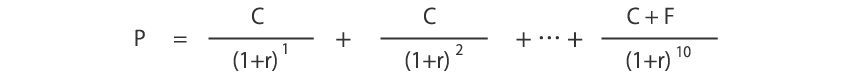
このrを求めることにより、債券の「利回り」を算出することになります。（ファイナンスの世界では「最終利回り」と呼ばれているようです。）

ところで、これまでの会計基準においてはこの利回りを割引率として使用することが通例でしたが、はたして、この利回りは退職給付債務計算において10年後のキャッシュフローを割り引いてくるのに適した率と言えるのでしょうか。

というのも、償還までに定期的にクーポンが支払われるため、実際にはより短い期間の利回りになっているのではないかという疑問が生じるのです。

そこで、クーポンのない債券（割引債）の利回り、すなわちスポットレートの方が適しているということになります。もし割引債があれば下の単純な式で利回りが求められるわけです。

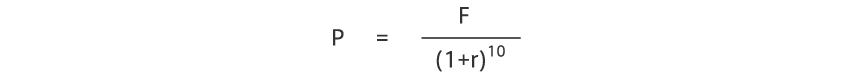
ところが、割引債は十分な流通量があるわけではなく、ほしい年限の債券が必ずしもあるわけではありません。また仮に存在したとしても、個別銘柄における誤差が生じる可能性があります。

そこで、t年のスポットレートをrtとしたときに、実際に流通している利付債のクーポンを割引債の集まりであると考え、以下の算式を立てます。

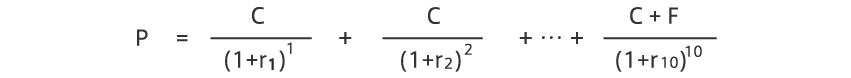
市場に流通している、たくさんの年限の債券の債券価格Pとクーポン価格C、額面Fからrtを推定したものがスポットレートのイールドカーブになります。

具体的な算出方法については、公益社団法人日本年金数理人会の「退職給付会計に関する数理実務ガイダンス」に以下のモデルが示されておりますが、きわめて専門的であり、各事業主は金融機関や弊社のようなコンサルティング会社から入手するのが一般的です。

● ネルソン・シーゲル・モデル
● スヴェンソン・モデル
● 多項スプライン・指数スプライン・Bスプライン

なお、ガイダンスには例示されていないものの、わかりやすい手法として、短い年限から順番に利回りを算定していく「ブートストラップ法」を採用されている例もあるようです。

ただしこちらの手法は、短い年限におけるスポットレートのずれが後の年限の計算に影響を及ぼし、なおかつ長い年限になるほど誤差が大きくなると一般的に言われており、注意が必要です。