平均余命はどう計算されているか

平均余命の定義

平均余命の定義を最初に説明します。

まず、平均余命は年齢ごとに定まります。x歳の平均余命とは、現在x歳の人が平均してあと何年生きるかを表す数値です。平均と言いましたが、数学的に言うと期待値というものです。そこでまず期待値について簡単に説明します。

期待値とは

サイコロを振ります。さて、このとき平均していくつくらいの目が出るでしょうか？

1とか6とか答える人はいないと思いますが、(1+6)÷2で3.5くらいかな、という人はいそうな気がします。この場合の答えは3.5で合っているのですが、計算式としては1×1/6+2×1/6+3×1/6+4×1/6+5×1/6+6×1/6=3.5というものが正しいです。

何をやっているのかというと、すべてのケース（1が出る、2が出る、…、6が出る）にそのケースが起こる確率（今の場合は全て1/6）を掛けた上で全て足しているのです。

余談ですが、退職給付債務もこの期待値の塊のようなものになっています。

生命表

平均余命の話をしていたのでした。上の方法で平均余命、つまりあと何年生きるかの期待値、を計算するには、1×(1年後に死亡する確率)+2×(2年後に死亡する確率)+…というような計算をすればよいということになります。

実際には1年後とか2年後といったキリのいい期間で死亡するとは限らないので、適当なモデルを設定することが必要となります。その状況をまとめた生命表というものを次に紹介します。

せっかくなので本物をみていただくのがよいでしょう。

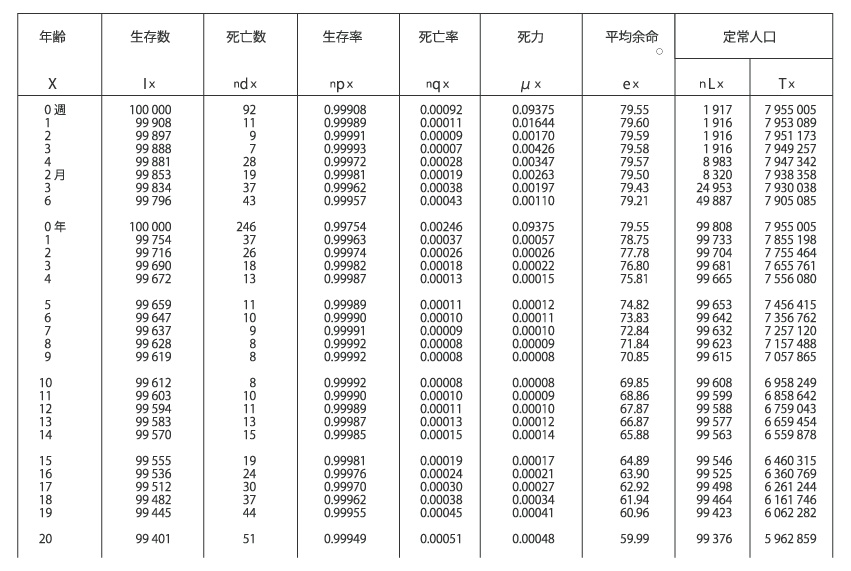
以下に掲げるのは　厚生労働省による第21回生命表（男子）です。

右から3列目にこのコラムの目的である平均余命が載っています。詳しすぎる情報も含まれていますが、基本的に左の3列と一番右の列だけで今回の話は済みます。細かいことですが平均余命にもいくつか種類があって、ここに記載されているのは完全平均余命というものです。

このコラムでは完全平均余命のことを単に平均余命と言っています。

一番上のほうは新生児の死亡率が高いため特別扱いしてあります。今回ここは無視しましょう。

上から9行目の0年というところからご覧ください。一番左の列は年齢です。左から2番目の列はある時点で生存しているちょうどx歳の人の数です。

左から3番目の列はそのうち翌1年の間に死亡する人の数です。死亡のタイミングは本来バラバラのはずですが、平均して全員期央に死亡すると考えます。

この表は上から下に時間が流れていくかのように読めます。ある時点でちょうど0歳の人が100,000人いたとします。そこから半年後にそのうち246人が死亡します。その半年後、つまりスタートから1年が経過した時点ではちょうど1歳の人が99,754人生存していることになります。これを生存者が0になるまで続けていきます。

実際の生命表は110歳（女子は114歳）まで作られています。もう一年やってみましょう。ちょうど1歳の人が99,754人います。半年後に37人死亡します。その半年後にはちょうど2歳の人が99,717人生存していることになります。

ここで人数が上の表と1人ずれてしまいました。今の説明は簡単のため離散的に考えていますが、本当は連続的に計算しているためだと思われます（足し算引き算ではなく、微分積分を使っているのではないかと思います）。

なお、この生命表は国勢調査の統計を基に作成されていますが、最も基本となる数値は左から5番目の列にある死亡率です。この率が統計を基に算出されています。年齢ごとの死亡率が与えられると、ある時点でちょうどx歳の人の人数にx歳の死亡率をかけることで翌1年の間に死亡する人の数がわかります。

なので、スタートにあたるちょうど0歳の人の人数（上の生命表では100,000人）を指定してやれば、翌1年間の死亡数は100,000×0.00246=246人、1年後の生存数は100,000-246=99,754人、翌1年間の死亡数は99,754×0.00037=37人…と上から順に生存数と死亡数を求めていくことで生命表を再現することができます。

平均余命の計算1

0歳の平均余命を平均寿命と言いますが、これを計算するにはどうすればいいかを考えてみましょう。

それには、ある時点でちょうど0歳の人があと何年生存するかについての期待値を求めることになります。これをさきほどのサイコロと同じように行うには、n年生存する確率がすべてのnについてわかればOKです。

つまり、1×(1年後に死亡する確率)+2×(2年後に死亡する確率)+…という計算をすべてのnに対して行うのです。すべてのnと言っても、200年も生きる人はいないので、実際には120くらいです。

さて、ではn年後に死亡確率とはどう求めるのか？上の生命表に即して考えましょう。

ある時点でちょうど0歳の人が100,000人います。このうち246人は0年後から1年後の間に死亡します。つまり、ちょうど0歳の人が0年から1年の間に死亡する確率は246÷100,000=0.00246である、と言えます。

同様に、ちょうど0歳の人が1年後から2年後の間に死亡する確率は37÷100,000=0.00037となります（37÷99,716ではないことに注意してください。こちらの計算では「ちょうど1歳の人が0年後から1年後の間に死亡する確率」になってしまいます）。

このようにして、2年後から3年後の間に死亡する確率は、3年後から4年後の間に死亡する確率は…という風にすべてのnについてn年後からn+1年後の間に死亡する確率が生命表から読み取れます。

こうなれば後は上の式にしたがって平均寿命が計算できます。スタートを0歳でなくx歳として同様の計算を行えば、x歳での平均余命が計算できます。

定常人口

これで満足してもよいのですが、よく使われるのはもう少し工夫した方法です。

生命表の一番右の列の数値を左から2列目の生存数で割ってみてください。すると平均余命が出るという仕組みになっています。1歳のところでやってみると、7,855,198÷99,754≒78.75と確かになっています。

ここで出てきた一番右の列の数値は、x歳以上の定常人口というものです。さきほど生命表は上から下に時間が流れていくように読めると言いましたが、集団の人口の定常状態を表しているとも読めます。つまり、ある時点でちょうど0歳の人が100,000人、ちょうど1歳の人が99,754人、…いる集団を考えます。

そして、1年たつごとにちょうど0歳の人が100,000人新しくこの集団に入ってくると考えます。集団の中の個々人は入れ替わっていくのだけれど各年齢の人数は変わらないという状態です。この定常状態でのx歳以上の人数のことをx歳以上の定常人口と言います。

単純に考えると、x歳以上の定常人口はx歳以上の生存数を全て足し合わせたものになるはずです。しかし、実際にExcelファイルをダウンロードしてSUM関数を使ってこの計算をしてみても一致しません。

さきほど触れたように、今は簡単のために離散的なモデルを考えて生命表を読んでいますが、実際の生命表は離散的にではなく連続的に計算している（足し算ではなく積分をしている）ためではないかと思います。

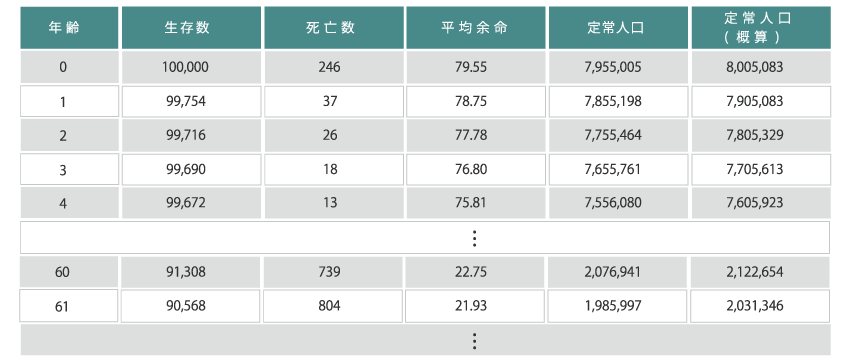
実際に計算してみた結果は次の表のようになりました。一番右の列がExcelで実際にx歳以上の生存数を足し合わせた結果で、その他の列は生命表の数字を抜粋しています。

平均余命の計算2

平均余命を簡単に計算するには、定常人口を生存数で割ればよい。しかし、生命表の定常人口は連続的に計算されているため、生存数の単純な合計とは合わない。したがって、この方法で生存数と死亡数から平均余命の計算をすることはできないのでは？という状況になりました。

ところが、生存数の合計から平均余命を近似計算することができます。それには、x+1歳以上の生存数の合計÷x歳の生存数+0.5とすればよいのです。

例えば0歳の平均余命（平均寿命）を上の表の数値から計算してみると、7,905,083÷100,000+0.5≒79.55となり確かに合っています。60歳の平均余命であれば、2,031,346÷91,308+0.5≒22.75となり、やはり合っています。この方法ならば、あまり複雑な算式を使わずに、与えられた死亡率からExcelで生命表を作って平均余命を概算することができます。

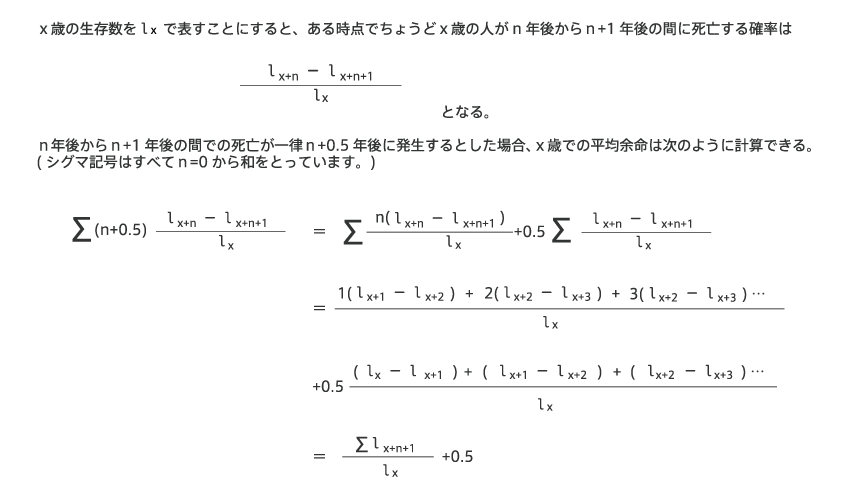
なぜこの計算方法でいいのか疑問に思われる方もみえると思うので、コラムの最後に数式による証明をつけておきます。

まとめ

以上、死亡率が与えられたときの生命表、そして平均余命の計算の仕方を解説してきました。

実際に自分で平均余命を計算しないといけない状況にある、という方は少ないかと思いますが、平均余命という数値を扱っている方はそれなりにみえるかと思います。計算方法を知ることで少しでも平均余命という数値に親しんでいただけたならば幸いです。

また、死亡に限らず、一般にある集団から何らかの原因により人が脱退していくという場合にもこの考え方は使うことができます。その場合の生命表にあたるものは脱退残存表と呼ばれます。

例えば、企業の従業員という集団からの退職による脱退を考えるという場合、平均余命にあたるものは平均残存勤務年数ということになります。興味を持たれた方は是非Excel等で実際に計算してみてください。

平均余命の計算1と2が同じであることの証明